$ \newcommand{\CF}{\mathcal{F}} \newcommand{\CI}{\mathcal{I}} \newcommand{\CJ}{\mathcal{J}} \newcommand{\CL}{\mathcal{L}} \newcommand{\CX}{\mathcal{X}} \newcommand{\CP}{\mathcal{P}} \newcommand{\CR}{\mathcal{R}} \newcommand{\CU}{\mathcal{U}} \newcommand{\RR}{\mathbb{R}} \newcommand{\NN}{\mathbb{N}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\ra}{\rightarrow} \newcommand{\la}{\leftarrow} \newcommand{\inv}{^{-1}} \newcommand{\maximize}{\mbox{maximize }} \newcommand{\minimize}{\mbox{minimize }} \newcommand{\subto}{\mbox{subject to }} \newcommand{\tr}{^{\intercal}} $
Benders Decomposition and Delayed Constraint Generation¶
We reserve this lecture to Benders decomposition method. We shall first start with a general framework as proposed by Benders (1962). Then, our focus will be on linear problems. We conclude this lecture by discussing the relationship between this lecture and the past two lectures.
General Case¶
Suppose we have an optimization problem given by
$$ \tag{P} \begin{array}{ll} \minimize & c\tr x + f(y)\\ \subto & Ax + F(y) \geq b, \\ & x \geq 0, y \in Y, \end{array} $$where $A$ is $m \times n$, $f:\RR^q \mapsto \RR$, $F:\RR^q \mapsto \RR^m$ and $Y \subseteq \RR^q$. The difficulty in this problem comes from the $y$ variables as the problem becomes a linear program for a fixed $y$. In a typical application the set $Y$ can also be complicated like the integrality constraints. This type of formulation arises frequently in stochastic programming, where the decision variables $x$ represent the activities in the future. As the uncertainty in the future reveals itself, the variable $y$ is altered and the corresponding expected cost, denoted as $f(y)$, is minimized.
We can, in fact, rewrite problem (P) in the following form:
$$ \begin{array}{ll} \minimize & f(y) + g(y)\\ \subto & y \in Y, \end{array} $$where $$ \tag{BSP} \begin{array}{rclll} g(y) & = & \minimize & c\tr x\\ & & \subto & Ax \geq b - F(y), \\ & & & x \geq 0. \end{array} $$
As we have observed before, if we fix $y$, then finding $g(y)$ is just solving a linear program. We call this LP as the Benders subproblem. To take the dual of (BSP), let $u \in \RR^m$ be the dual variables associated with its constraints. Then, the dual Benders subproblem becomes
$$ \tag{DBSP} \begin{array}{rclll} g(y) & = & \maximize & (b - F(y))\tr u\\ & & \subto & A\tr u \leq c, \\ & & & u \geq 0. \end{array} $$Here is a key observation: The feasible region of (DBSP) is independent of the $y$ variables. This implies that if the feasible region of (DBSP) is empty, then either the feasible region of (BSP) is empty or its optimal objective function value is unbounded. In the former case, the original problem (P) becomes infeasible whereas in the latter case, the optimal objective function value of problem (P) is also unbounded. Therefore, we can just assume that the feasible region of (DBSP) is not empty and hence, it can be written in terms of its extreme points and extreme directions by using the Minkowski's Representation theorem (see previous lecture).
Let $\CU$ be the feasible region of (DBSP) given by
$$ \CU = \{u \in \RR^m : A\tr u \leq c, \ u \geq 0\}, $$and denote its sets of extreme points and extreme rays by
$$ \CP_{\CU} = \{ u^p, p \in \CI_\CP\} \mbox{ and } \CR_{\CU} = \{ u^r, r \in \CI_\CR\}, $$respectively. Given $y$, suppose for an extreme ray $u^r$ that $(b - F(y))\tr u > 0$. This would imply that (DBSP) is unbounded, and hence, (BSP) is infeasible, which in turn makes (P) infeasible. So we can rewrite (DBSP) as follows:
$$ \begin{array}{rcllll} g(y) & = & \minimize & v & \\ & & \subto & (b - F(y))\tr u^p \leq v, & p \in \CI_\CP,\\ & & & (b - F(y))\tr u^r \leq 0, & r \in \CI_\CR. \end{array} $$Now we have a reformulation of (DBSP) with only one decision variable ($v$) but too many constraints. However, this model gives us a chance to rewrite the original problem (P) as
$$ \tag{BMP} \begin{array}{lll} \minimize & f(y) + v\\ \subto & (b - F(y))\tr u^p \leq v, & p \in \CI_\CP, \\ & (b - F(y))\tr u^r \leq 0, & r \in \CI_\CR, \\ & y \in Y. & \end{array} $$This problem is known as the Benders master problem. It impractical to generate all extreme points and extreme rays. Thus, Benders decomposition works with only a subset of those exponentially many constraints, and depending on the solution of the subproblem, adds more constraints iteratively until the optimal solution of (BMP) is attained. This procedure is known as delayed constraint generation. Let $\bar{\CI}_\CP \subseteq \CI_\CP$ and $\bar{\CI}_\CR \subseteq \CI_\CR$ designate the subsets of the considered constraints. Then, we can write the restricted Benders master problem:
$$ \tag{RBMP} \begin{array}{lll} \minimize & f(y) + v\\ \subto & (b - F(y))\tr u^p \leq v, & p \in \bar{\CI}_\CP, \\ & (b - F(y))\tr u^r \leq 0, & r \in \bar{\CI}_\CR, \\ & y \in Y. & \end{array} $$Suppose the optimal solution of (RBMP) is $(\bar{y}, \bar{v})$. Clearly, $f(\bar{y}) + \bar{v}$ is a lower bound on the optimal objective function value of (P). We next solve (DBSP) with fixed $\bar{y}$. There are three possible cases:
- If (DBSP) is unbounded, then we have extreme ray $u^r$ so that we can add the following constraint to the (RBMP): $$ % \tag{BFC} (b - F(y))\tr u^r \leq 0. $$ This type of constraints are known as Benders feasibility cuts as they imply the feasibility of problem (BSP), and consequently, of problem (P)
- If $\bar{v} < g(\bar{y})$ and (DBSP) is optimal, then we have an extreme point $u^p$ so that we can add the following constraint to the (RBMP): $$ % \tag{BOC} (b - F(y))\tr u^p \leq v. $$ This type of constraints are known as Benders optimality cuts. Moreover, $f(\bar{y}) + g(\bar{y})$ is an upper bound on the optimal objective function value of (P).
- When $\bar{v} = g(\bar{y})$, that is the lower bound is equal to the upper bound, the algorithm stops.
The following flowchart illustrates the steps for applying Benders decomposition
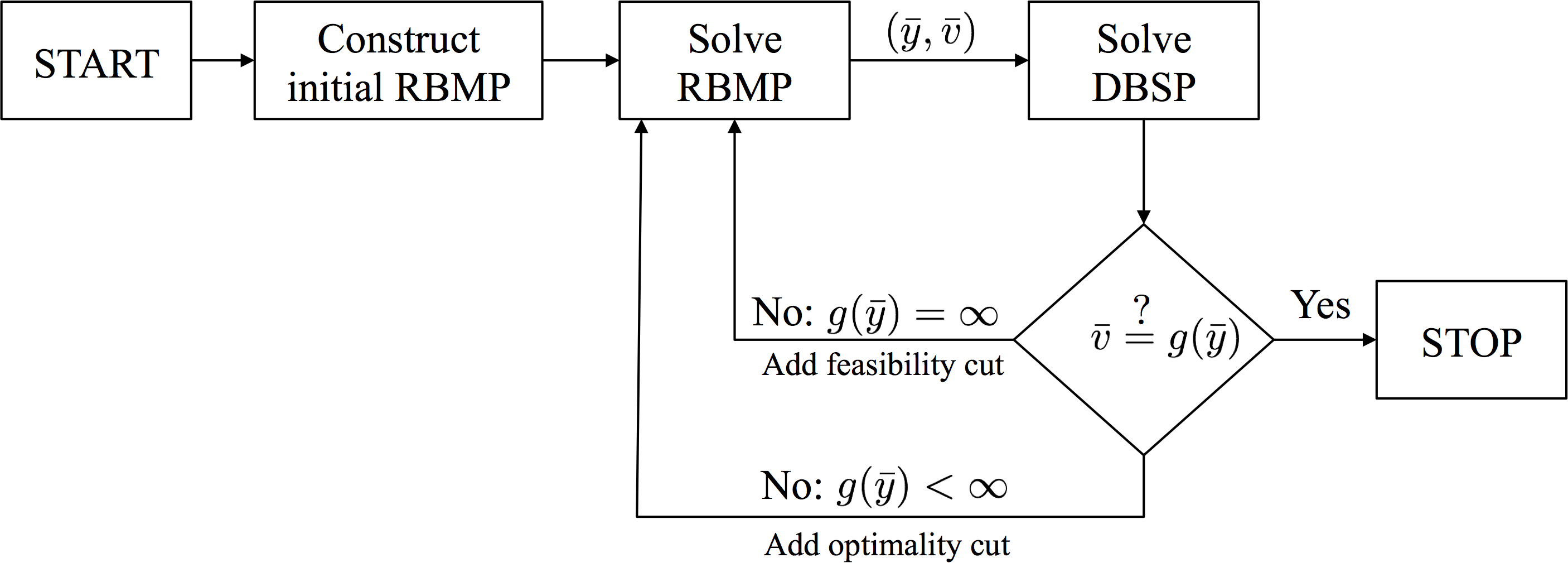
Roughly speaking this iterative algorithm converges to the optimal solution of (P) as we have finitely many extreme points and extreme rays (Benders, 1962). It is important to note that in practice, the algorithm is usually terminated whenever the difference between the upper bound and the lower bound is small enough.
Linear Case¶
Whenever the functions $f$ and $F$ are linear, then we can rewrite problem (P) as
$$ \begin{array}{ll} \minimize & c\tr x + d\tr y\\ \subto & Ax + By \geq b, \\ & x \geq 0, y \in Y, \end{array} $$where $B$ is an $m \times q$ matrix. Note in this case that the (BMP) becomes:
$$ \begin{array}{lll} \minimize & d\tr y + v\\ \subto & (b - By)\tr u^p \leq v, & p \in \CI_\CP, \\ & (b - By)\tr u^r \leq 0, & r \in \CI_\CR, \\ & y \in Y. & \end{array} $$If the set $Y$ is a polyhedron, then the (BMP), or equivalently the overall problem (P), becomes an LP problem. That does not look too exciting. However, if we keep $f$ and $F$ as linear functions but let $Y$ be a set of integer solutions, then we have a more interesting problem. For example, consider a numerical example for the matrix segmentation problem arising in Intensity Modulated Radiation Therapy treatment planning (Taşkın, 2010):
$$ \begin{array}{ll} \minimize & \sum_{j=1}^{5} x_j + \sum_{j=1}^{5} 7y_j \\ \subto & x_1 + x_4 + x_5 = 8, \\ & x_2 + x_5 = 3, \\ & x_3 + x_4 = 5, \\ & x_1 \leq 8y_1, x_2 \leq 3y_2, x_3 \leq 5y_3, x_4 \leq 5y_4, x_5 \leq 3y_5, \\ & x_j \geq 0, y_j \in \{0,1\}, \ j = 1, \dots, 5. \end{array} $$For a fixed $\bar{y}$, the Benders subproblem becomes
$$ \begin{array}{rcll} g(\bar{y}) & = & \minimize & \sum_{j=1}^{5} x_j \\ &&\subto & x_1 + x_4 + x_5 = 8, \\ &&& x_2 + x_5 = 3, \\ &&& x_3 + x_4 = 5, \\ &&& x_1 \leq 8\bar{y}_1, x_2 \leq 3\bar{y}_2, x_3 \leq 5\bar{y}_3, x_4 \leq 5\bar{y}_4, x_5 \leq 3\bar{y}_5, \\ &&& x_j \geq 0. \end{array} $$Using next the dual variables $u_1, \dots, u_8$, we can write the corresponding (DBSP)
$$ \begin{array}{rcll} g(\bar{y}) & = & \maximize & 8u_1 + 3u_2 + 5u_3 + 8\bar{y}_1 u_4 + 3\bar{y}_2u_5 + 5\bar{y}_3u_6 + 5\bar{y}_4u_7 + 3\bar{y}_5u_8\\ &&\subto & u_1 + u_4 \leq 1, \\ &&& u_2 + u_5 \leq 1, \\ &&& u_3 + u_6 \leq 1, \\ &&& u_1 + u_3 + u_7 \leq 1, \\ &&& u_1 + u_2 + u_8 \leq 1, \\ &&& u_j \leq 0, \ j=1, \dots, 5. \end{array} $$Denote the extreme points and the extreme rays of the feasible region of the dual subproblem by $u^p$, $p \in \CI_\CP$ and $u^r$, $r \in \CI_\CR$, respectively. Then, we obtain the (BMP):
$$ \begin{array}{lll} \minimize & \sum_{j=1}^{5} 7y_j + v &\\ \subto & 8u^p_1 + 3u^p_2 + 5u^p_3 + 8y_1u^p_4 + 3y_2u^p_5 + 5y_3u^p_6 + 5y_4u^p_7 + 3y_5u^p_8 \leq v, & p \in \CI_\CP,\\ & 8u^r_1 + 3u^r_2 + 5u^r_3 + 8y_1u^r_4 + 3y_2u^r_5 + 5y_3u^r_6 + 5y_4u^r_7 + 3y_5u^r_8 \leq 0, & r \in \CI_\CR,\\ & v \geq 0, \ y_j \in \{0,1\}, \ j = 1, \dots, 5. \end{array} $$Note that we add the trivial lower bound on $v$. Now we are ready to solve this problem with Benders decomposition. Initially, we start without any Benders cut. Our first (RBMP) is given as
$$ \begin{array}{ll} \minimize & \sum_{j=1}^{5} 7y_j + v \\ \subto & v \geq 0, \ y_j \in \{0,1\}, \ j = 1, \dots, 5. \end{array} $$Clearly, at the optimal $\bar{y}=0$ and $\bar{v}=0$. Then, we solve (DBSP) which yields an unbounded objective function value with an extreme ray $u^r = (2,-1,-1,-2,0,0,-1,-1)\tr$. This leads to a feasibility cut that we can use to form our new (RBMP):
$$ \begin{array}{ll} \minimize & \sum_{j=1}^{5} 7y_j + v \\ \subto & 8 - 16y_1 - 5y_4 - 3y_5 \leq 0, \\ &v \geq 0, \ y_j \in \{0,1\}, \ j = 1, \dots, 5. \end{array} $$The optimal solution of this restricted problem is $\bar{y} = (1,0,0,0,0)\tr$ and $\bar{v}=0$. We next solve the (DBSP) with $\bar{y}$ and observe that its optimal objective function value, $g(\bar{y})$ is unbounded. Then, an extreme ray is $u^r = (0,0,1,0,0,-1,-1,0)\tr$. We add another feasibility cut and form the next (RBMP):
$$ \begin{array}{ll} \minimize & \sum_{j=1}^{5} 7y_j + v \\ \subto & 8 - 16y_1 - 5y_4 - 3y_5 \leq 0, \\ & 5 - 5y_3 - 5y_4 \leq 0, \\ &v \geq 0, \ y_j \in \{0,1\}, \ j = 1, \dots, 5. \end{array} $$After solving new (RBMP), we obtain its optimal solution as $\bar{y} = (0,0,0,1,1)\tr$ and $\bar{v}=0$. Solving now (DBSP) with the new $\bar{y}$ yields an optimal objective function value of $g(\bar{y})=8 > \bar{v}$. Thus, we have a Benders optimality cut that can be added to the recent (RBMP).
$$ \begin{array}{ll} \minimize & \sum_{j=1}^{5} 7y_j + v \\ \subto & 8 - 16y_1 - 5y_4 - 3y_5 \leq 0, \\ & 5 - 5y_3 - 5y_4 \leq 0, \\ & 16 - 5y_4 - 3y_5 \leq v, \\ &v \geq 0, \ y_j \in \{0,1\}, \ j = 1, \dots, 5. \end{array} $$The optimal solution of this (RBMP) is $\bar{y} = (0,0,0,1,1)\tr$ and $\bar{v}=8$. As $\bar{y}$ has not changed, the optimal objective function value is still $g(\bar{y}) = \bar{v} = 8$. We have obtained the optimal solution.
Relationship with Dantzig-Wolfe Decomposition¶
Recall that we have started the previous section with an LP similar to the following one:
$$ \begin{array}{lll} \minimize & c\tr x + d\tr y &\\ \subto & Ax + By \geq b, & (u)\\ & x \geq 0, y \in Y &. \end{array} $$Here, the only difference is taking the set $Y$ as the first orthant. Let $u \in \RR^m$ be the dual variables corresponding to the first set of constraints. Then, the dual problem becomes
$$ \begin{array}{ll} \maximize & b\tr u \\ \subto & A\tr u \leq c,\\ & B\tr u \leq d,\\ & u \geq 0. \end{array} $$Using the previously defined set
$$ \CU = \{u \in \RR^m : A\tr u \leq c, \ u \geq 0\}, $$as well as its extreme sets
$$ \CP_{\CU} = \{ u^p, p \in \CI_\CP\} \mbox{ and } \CR_{\CU} = \{ u^r, r \in \CI_\CR\}, $$we can apply Dantzig-Wolfe decomposition to obtain the master problem
$$ \begin{array}{llr} \maximize & \sum_{p \in \CI_\CP}\mu_p(b\tr u^p) + \sum_{r \in \CI_\CR}\nu_r(b\tr u^r) &\\ \subto & \sum_{p \in \CI_\CP} \mu_p(B\tr u^p) + \sum_{r \in \CI_\CR} \nu_r(B\tr u^r) \leq d, & (y)\\ & \sum_{p \in \CI_\CP} \mu_p = 1, & (v)\\ & \mu_p \geq 0, p \in \CI_\CP, & \\ & \nu_r \geq 0, r \in \CI_\CR.& \end{array} $$If we now take the dual of this problem with the associated dual variables $y$ and $v$, then we obtain
$$ \begin{array}{lll} \minimize & d\tr y + v\\ \subto & (b - By)\tr u^p \leq v, & p \in \CI_\CP, \\ & (b - By)\tr u^r \leq 0, & r \in \CI_\CR, \\ & y \in Y. & \end{array} $$This is exactly the restricted master problem in the linear case of Benders decomposition.
This establishes that Benders decomposition is equivalent to applying Dantzig-Wolfe decomposition to the dual of original problem (P). In the previous lecture, we have also discussed the relationship between the Lagrangean dual problem and the Dantzig-Wolfe decomposition. To sum up, we have shown that the following are equivalent:
- Cutting plane method applied to the Lagrangian dual problem.
- Dantzig-Wolfe decomposition applied to the original problem.
- Benders decomposition applied to the dual of the original problem.
Concluding Remarks¶
In all our examples above, the subproblems have always been linear programs, and hence, we have extracted the dual information from those subproblems easily. However, if the subproblem is nonlinear but satisfies some necessary convexity assumptions so that strong duality condition hold, then one can still solve the subproblems within Benders decomposition approach.
In this lecture, we have not used GNU Octave to solve our example problem because the GNU Octave interface of GLPK does not provide an access to the extreme rays for unbounded problems. Gurobi is another optimization software that could be used. Unfortunately, they provide only a MATLAB interface which does return the extreme rays.
Papers for Next Week's Discussion¶
- Benders, J. F. (1962). Partitioning procedures for solving mixed-variables programming problems, Numerische Mathematik, 4, 238-252.
- Geoffrion, A. M. and G. W. Graves (1974). Multicommodity distribution system design by Benders decomposition, Management Science, 20:5, 822-844.
- Contreras, I., Cordeau J.-F. and G. Laporte (2011). Benders decomposition for large-scale uncapacitated hub location, 59:6, 1477-1490.